Recently, we are working on optimizing a class of non-convex objectives with a celebrated and general structure, called continuous submodularity. People know that submodularity is a classical structure in combinatorial optimization, it turns out that continuous submodularity is also a common non-convex structure for many continuous objectives, with strong guarantees for both minimization and maximization.

For two very recent papers in this area, one can refer to the one from Francis Bach for minimization, and the one from us for maximization. This post aims to: i) explain how to recognize submodular continuous-functions; ii) summarize the current results on optimizing submodular continuous-functions; iii) discuss open problems in this new area.

Generic submodular functions

To have a better understanding of the submodularity of both set-functions and continuous-functions, let us first of all give a generic view on the submodular functions.

The domain of a “generic” submodular function $f: \cal X\rightarrow \mathbb R$ is the Cartesian product of subsets of $\mathbb{R}$: $\cal X = \prod_{i=1}^n \cal X_i$, each $\cal X_i$ is a compact subset of $\mathbb R$. It is clear that one can define a lattice over $\cal X$ by taking the “join” operation $\vee$ as coordinate-wise maximum, and the “meet” operation $\wedge$ as coordinate-wise minimum, respectively.

By considering different realizations of $\cal X_i$, we can recover different submodular functions:

• $\cal X_i = \{0, 1\}$: submodular set-function;
• $\cal X_i = \{0, 1, …, k_i -1\}, k_i>2$, $k_i\in \mathbb Z$: submodular integer-lattice-function;
• $\cal X_i = [a, b]$ is an interval: submodular continuous-function.

The submodularity of all of them can be defined as:

Submodularity and submodular functions: For all $(x,y)$ in the domain, it holds $f(x) + f(y) \geq f(x\vee y) + f(x\wedge y)$. This function $f$ is a submodular function.

It is well-known that for set-functions, submodularity is equivalent to the diminishing returns (DR) property. However, this does not hold when generalized to generic functions defined over $\cal X$:

DR property & DR-submodular functions: Let $\chi_i$ be the $i^\text{th}$ characteristic vector. $f$ satisfies the DR property if $\forall a\leq b\in \cal X$, for any coordinate $i$, $\forall k\in \mathbb{R}_+$ s.t. $k\chi_i+a$ and $k\chi_i+b$ are still in $\cal X$, it holds $f(k\chi_i+a) - f(a) \geq f(k\chi_i+b) - f(b)$.
This function $f$ is called a DR-submodular function.

One immediate observation is that $\nabla f(a)\geq \nabla f(b)$ (if $f$ is differentiable), so the gradient of a differentiable DR-submodualr function is an antitone mapping.

Both submodular and DR-submodular functions are prevalent in real-world applications. So far there are naturally three questions:

Q1. For generic functions defined over $\cal X$, submodularity $\neq$ DR, what is the connection between them?

Q2. For the submodularity of generic functions defined over $\cal X$, is there an equivalent diminishing-returns-style property to characterize it?

Q3. What we can say regarding optimizing submodular and DR-submodular continuous-functions?

These questions will be answered in the following.

Characterization of generic submodular functions

First of all, we give a positive answer to question Q2 by proposing the weak DR property:

weak DR: $f$ satisfies the weak DR property if $\forall a\leq b\in \cal X$, for any coordinate $i\in \{i’| a_{i’} = b_{i’} \}$, $\forall k\in \mathbb{R}_+$ s.t. $k\chi_i+a$ and $k\chi_i+b$ are still in $\cal X$, it holds $f(k\chi_i+a) - f(a) \geq f(k\chi_i+b) - f(b)$.

and show that

Lemma: For a generic function $f$, weak DR $\Leftrightarrow$ submodularity.

For question Q1, now it is clear that DR-submodular functions are a subclass of submodular functions. Furthermore, it can be shown that,

Lemma: submodularity + coordinate-wise concavity $\Leftrightarrow$ DR.

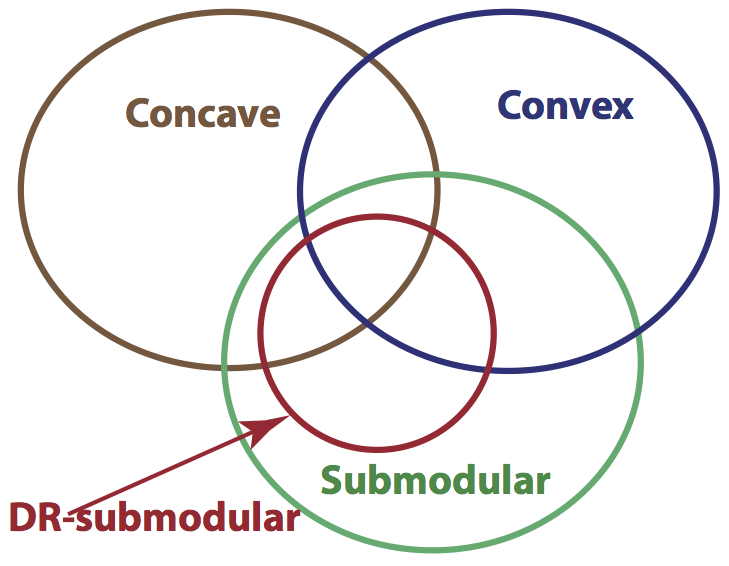The class of submodular continuous-functions contains a subset of both convex and concave functions, see the left figure for an illustration. For detailed examples, one can refer to the corresponding sections in the above the two papers.

The characterizations of submodular and DR-submodular continuous-functions can be put in comparison with that of convex functions, which are summarized in the following tables. These properties make it very easy to recognize the submodularity of a continuous-function.

For question Q3, please see the following.

What we can say about optimizing submodular continuous-functions so far?

Here I just summarize the current results on minimizing and maximizing submodular continuous-functions from the above two papers. It is noteworthy that there are plenty of open problems in this new area.

• Submodular continuous-functions over the “box” constraints can be minimized to arbitrary precision in polynomial time using the discretization + continuous extension method in Bach 2015.

• Maximizing a monotone DR-submodular continuous-function over general down-closed convex constraints is NP-hard. The submodular Frank-Wolfe algorithm gives $(1-1/e)$-approximation and sublinear “convergence” rate Bian et al 2016.

• Maximizing a non-monotone submodular continuous-function over “box” constraints is NP-hard. The generalized DoubleGreedy algorithm gives $1/3$-approximation Bian et al 2016.

Open problems

Continuous submodularity is a very general structure in the non-convex realm. The characterizations, especially the second order properties, give a very convenient way to recognize a submodular/DR-submodular objective in real-world applications. So in terms of new applications, I think there are much more non-convex objectives waiting to be discovered, like what happened for the submodular set-functions.

In terms of theory, there are lots of interesting open problems. To name a few:

• For the minimization, how to make the algorithm faster/scalable? How to properly utilize the gradient information?

• What one can say about constrained minimization?

• For maximization, the projected gradient method works good in the experiments, is it possible to prove some approximation guarantees?

• For maximizing a non-monotone submodular continuous-function over “box” constraints, whether the worst-case guarantee or the hardness results can be improved?

---

Hopefully you will find out that the non-convex problem you are working on turns out to be a submodular/DR-submodular one!